Сумма углов 360° является характерной особенностью нескольких геометрических фигур. Это важное свойство широко используется в геометрии и на практике.
Содержание
Сумма углов 360° является характерной особенностью нескольких геометрических фигур. Это важное свойство широко используется в геометрии и на практике.
Геометрические фигуры с суммой углов 360°
| Фигура | Пояснение |
| Четырехугольник | Любой выпуклый четырехугольник |
| Параллелограмм | Частный случай четырехугольника |
| Прямоугольник | Все углы по 90°, 4×90°=360° |
| Ромб | Противоположные углы равны |
| Трапеция | Сумма углов при каждой боковой стороне 180° |
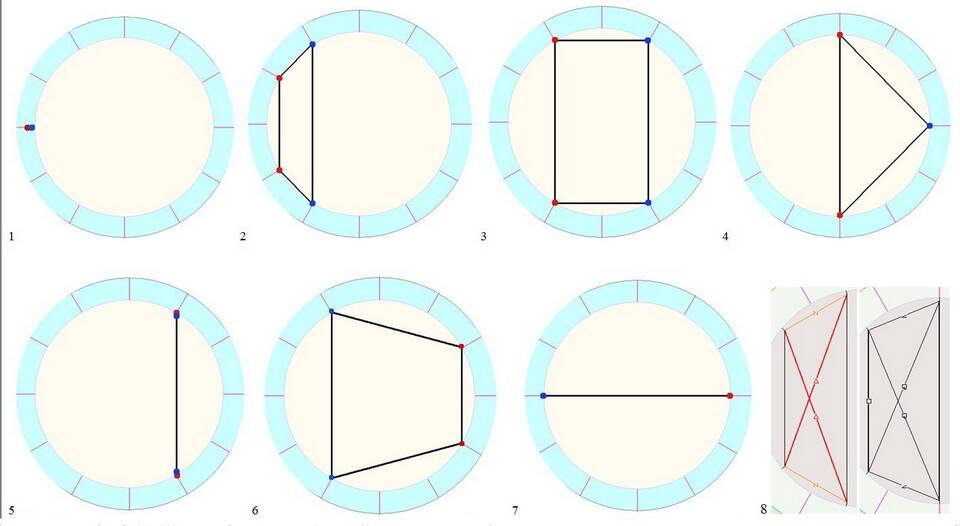
Доказательство для четырехугольника
- Проводим диагональ в четырехугольнике
- Получаем два треугольника
- Сумма углов каждого треугольника 180°
- 2×180°=360° - сумма всех углов четырехугольника
Примеры расчета
- Квадрат: 4 угла по 90° = 360°
- Прямоугольник: 4 угла по 90° = 360°
- Ромб с углами 60° и 120°: 2×60° + 2×120° = 360°
Практическое значение
Знание о сумме углов в 360° применяется в архитектуре, строительстве, проектировании и других областях. Это свойство помогает правильно рассчитывать конструкции и проверять геометрические построения.
Интересные факты
- Сумма внешних углов любого выпуклого многоугольника равна 360°
- В круге 360°, что связано с древними системами счисления
- Это свойство используется в навигации и астрономии
