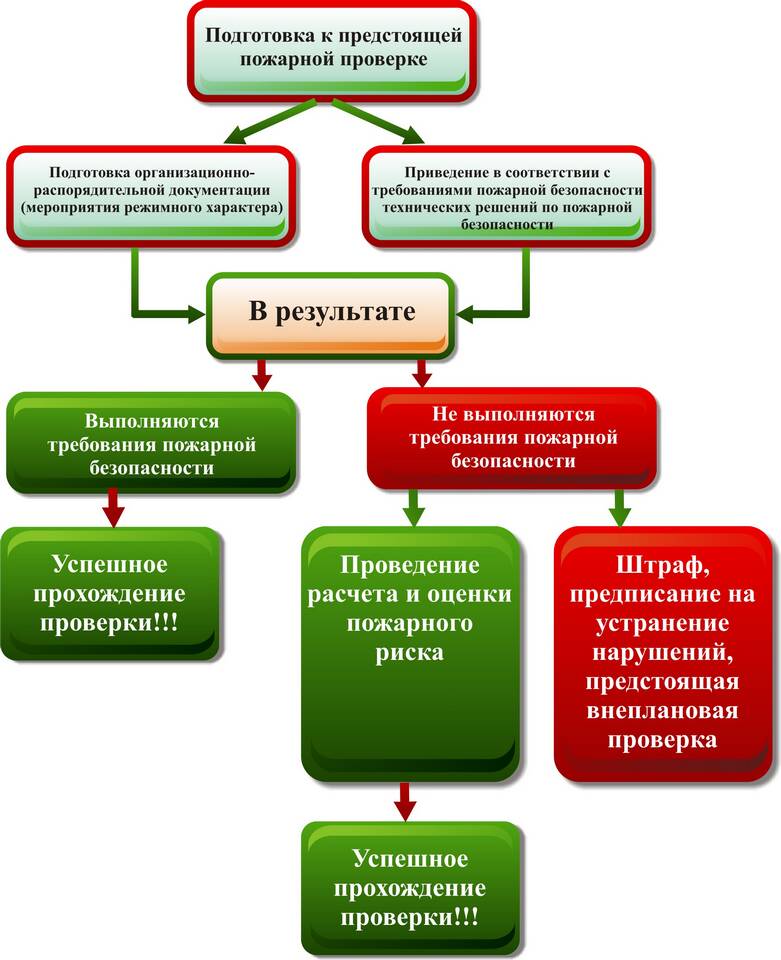
В теории вероятностей важное место занимает вычисление вероятности суммы событий. Рассмотрим основные формулы и методы расчета для различных случаев.
Содержание
Формула вероятности суммы двух событий
Для любых двух событий A и B вероятность их суммы вычисляется по формуле:
| Формула | P(A ∪ B) = P(A) + P(B) - P(A ∩ B) |
| Где: |
|
Частные случаи
Несовместные события
Если события не могут произойти одновременно (A ∩ B = ∅):
| Формула | P(A ∪ B) = P(A) + P(B) |
| Пример | Вероятность выпадения 1 или 6 на игральной кости: 1/6 + 1/6 = 1/3 |
Независимые события
Если наступление одного события не влияет на вероятность другого:
| Формула | P(A ∪ B) = P(A) + P(B) - P(A) × P(B) |
| Пример | Вероятность выпадения хотя бы одной решки при двух бросках монеты: 0.5 + 0.5 - 0.5×0.5 = 0.75 |
Вероятность суммы трех событий
Для трех событий A, B и C формула принимает вид:
| Формула | P(A∪B∪C) = P(A) + P(B) + P(C) - P(A∩B) - P(A∩C) - P(B∩C) + P(A∩B∩C) |
Общая формула для n событий
Для произвольного числа событий используется принцип включений-исключений:
- Сумма вероятностей отдельных событий
- Минус суммы вероятностей всех парных пересечений
- Плюс суммы вероятностей тройных пересечений
- И так далее, с чередованием знаков
Примеры решения задач
Пример 1: Карты из колоды
Какова вероятность вытащить туза или червовую карту из стандартной колоды (52 карты)?
| Решение |
|
Пример 2: Работа приборов
Вероятность отказа первого прибора 0.1, второго - 0.2. Какова вероятность отказа хотя бы одного прибора, если они работают независимо?
| Решение |
|
Практическое применение
Формулы вероятности суммы событий используются в:
- Страховых расчетах
- Оценке надежности технических систем
- Статистических исследованиях
- Финансовом анализе рисков
- Теории массового обслуживания
Правильное применение этих формул позволяет точно оценивать вероятности сложных событий, состоящих из нескольких компонентов.